Weighted average: definition and relationship with $\chi ^2$

A weighted average is the result of the special case of a data fitting to a model function which is a constant. It is easy to see that minimizing w.r.t $x$

$$\chi^2 = \mathop{\sum}_{j=1}^{N_{\mathrm{obs}}} {\ensuremath{\dis... ...h{\left({x-O_j}\right)}}^2 }}}}{{\ensuremath{\displaystyle{ \sigma_j^2 }}}}}}}$$

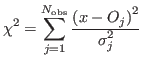
yields

$$x= \langle x \rangle_{\!\mathrm{w}}={\ensuremath{\displaystyle{\f... ...th{\displaystyle{1 }}}}{{\ensuremath{\displaystyle{ \sigma_j^2 }}}}}}} }}}}}}}$$

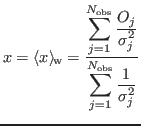
The good-faith s.d. (square-root of twice the inverse of the second derivative of $\chi ^2$ at the minimum) is then

$$\sigma_{\langle x \rangle_{\!\mathrm{w}}} = {\ensuremath{\display... ...h{\displaystyle{1 }}}}{{\ensuremath{\displaystyle{ \sigma_j^2 }}}}}}} }}}}}}}}$$

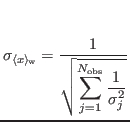
I use the term 'good-faith' to indicate the case when it is really appropriate to use a constant as a model functions, i.e. when the observations are truly different observations of the same observable. When this is not the case but we do not know what to do better we can at least increase the s.d. In fact, there is a correction factor for the s.d., given - in this case - by

$$\mathsf{GoF}= \sqrt{ {\ensuremath{\displaystyle{\frac{{\ensuremat... ... }}}}}}} }}}}}}} }}}}{{\ensuremath{\displaystyle{ N_{\mathrm{obs}}-1 }}}}}}} }$$

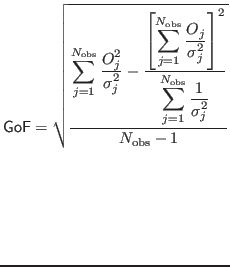
so that

$${\sigma}_{\langle x \rangle_{\!\mathrm{w}}}^{\mathrm{corrected}} = \mathsf{GoF}\ \sigma_{\langle x \rangle_{\!\mathrm{w}}}$$

Specializing now to the two cases above,