Basic binning

1.

We have several patterns, say $P$ . Each $k$ -th pattern, for $k=1,\ldots,P$ , is constituted by $N_k$ angular intervals in the diffraction angle $2\theta\equiv{\ensuremath{{2\theta}}}$ :

$$b_{k,j}={\ensuremath{\left[{{\ensuremath{{2\theta}}}_{k,j}^{-},{\ensuremath{{2\theta}}}_{k,j}^{+}}\right]}},\qquad j=1,\ldots,N_k$$

of center

$$\hat{b}_{k,j}={\ensuremath{\displaystyle{\frac{{\ensuremath{\disp... ...{+}+{\ensuremath{{2\theta}}}_{k,j}^{-}}}}}{{\ensuremath{\displaystyle{2}}}}}}}$$

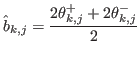
and width

$${\ensuremath{\left\vert{b_{k,j}}\right\vert}}={\ensuremath{{2\theta}}}_{k,j}^{+}-{\ensuremath{{2\theta}}}_{k,j}^{-}$$

To each interval is associated a counting $C_{k,j}$ , an efficiency correction factor $e_{k,j}$ , a monitor $m_{k,j}$ (ionization chamber times acquisition time). All 'bad' intervals have been already flagged down and discarded. Efficiency corrections and monitors are supposed to be normalized to a suitable value. Note that intervals $b_{k,j}$ might have multiple overlaps and might not cover an compact angular range.

2.

Following Mighell's statistics[6] and normal scaling procedures, we first transform those numbers into associated intensities, intensity rates and relevant s.d.:

$$I_{k,j}={\ensuremath{\displaystyle{\frac{{\ensuremath{\displaysty... ...nsuremath{\left({C_{k,j}+\min{\ensuremath{\left({1,C_{k,j}}\right)}}}\right)}}$$

$$\sigma_{I_{k,j}}={\ensuremath{\displaystyle{\frac{{\ensuremath{\d... ...ath{\displaystyle{m_{k,j}}}}}}}}\sqrt{{\ensuremath{\left({C_{k,j}+1}\right)}}}$$

$$r_{k,j}={\ensuremath{\displaystyle{\frac{{\ensuremath{\displaysty... ...nsuremath{\left({C_{k,j}+\min{\ensuremath{\left({1,C_{k,j}}\right)}}}\right)}}$$

$$\sigma_{r_{k,j}}={\ensuremath{\displaystyle{\frac{{\ensuremath{\d... ...k,j}}\right\vert}}m_{k,j}}}}}}}}\sqrt{{\ensuremath{\left({C_{k,j}+1}\right)}}}$$

3.

We set up the final binned grid, composed of $M$ binning intervals

$$B_\ell=[{\ensuremath{{2\theta}}}_0+(\ell-1)B, {\ensuremath{{2\theta}}}_0+\ell B],\qquad \ell=1,\ldots,M$$

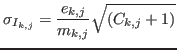
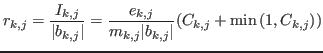
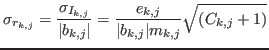
all contiguous and each having the same width

$${\ensuremath{\left\vert{B_\ell}\right\vert}}=B$$

and each centered in

$$\hat{B}_\ell={\ensuremath{{2\theta}}}_0+(\ell-1/2)B,$$

covering completely the angular range between ${\ensuremath{{2\theta}}}_0$ and ${\ensuremath{{2\theta}}}_{max}={\ensuremath{{2\theta}}}_0+MB$ .

4.

For bin $\ell$ , we consider only and all the experimental intervals

$$b_{k,j}$$   such that$$\qquad {\ensuremath{\left\vert{ b_{k,j}\cap B_\ell }\right\vert}} > 0.$$

More restrictively, one may require to consider only and all the experimental intervals

$$b_{k,j}$$   such that$$\qquad \hat{b}_{k,j}\in B_\ell .$$

5.

In order to estimate the rate in each $\ell$ -th bin, we use all above selected rate estimates concerning bin $B_\ell$ and we get a better one with the weighted average method.
In the weighted average method, we suppose to have a number $N_E$ of estimates $O_n$ of the same observable $O$ , each one with a known s.d. $\sigma_{O_n}$ and each (optionally) repeated with a frequency $\nu_n$ . Then

$$\langle O\rangle ={\ensuremath{\displaystyle{\frac{{\ensuremath{\... ...remath{\displaystyle{ \mathop{\sum}_{n=1}^{N_E}\nu_n \sigma_{O_n}^{-2} }}}}}}}$$

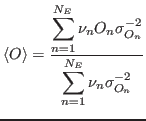
Clearly the place of the frequencies in our case can be taken by coefficients

$${\ensuremath{\displaystyle{\frac{{\ensuremath{\displaystyle{{\ens... ...ert{ b_{k,j}\cap B_\ell }\right\vert}}}}}}{{\ensuremath{\displaystyle{B}}}}}}}$$

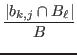
that weigh the $k,j$ -th estimate by its relative extension within bin $B_\ell$ .

6.

Now we can simply accumulate registers

$$X_\ell=\mathop{\sum_{k,j}}_{ {\ensuremath{\left\vert{ b_{k,j}\cap... ...aystyle{B}}}}}}}\ r_{k,j}\ {\ensuremath{\left({\sigma_{r_{k,j}}}\right)}}^{-2}$$

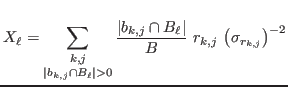
and

$$Y_\ell=\mathop{\sum_{k,j}}_{ {\ensuremath{\left\vert{ b_{k,j}\cap... ...th{\displaystyle{B}}}}}}}\ {\ensuremath{\left({\sigma_{r_{k,j}}}\right)}}^{-2}$$

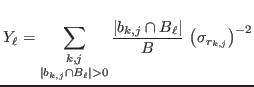
so that we can extract an intensity rate estimate (counts per unit diffraction angle and per unit time at constant incident intensity) as

$$R_\ell={\ensuremath{\displaystyle{\frac{{\ensuremath{\displaystyle{X_\ell}}}}{{\ensuremath{\displaystyle{Y_\ell}}}}}}};$$

$$\sigma_{R_\ell}={\ensuremath{\displaystyle{\frac{{\ensuremath{\displaystyle{1}}}}{{\ensuremath{\displaystyle{\sqrt{Y_\ell}}}}}}}}.$$

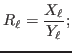
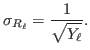
Now optionally we can transforms rates in intensities (multiplying both $R_\ell$ and $\sigma_{R_\ell}$ by $B$ ). We can use any other scaling factor $K$ as we wish instead of $B$ . The best cosmetic scaling is the one where

$$\mathop{\sum}_{\ell=1}^M{\ensuremath{\displaystyle{\frac{{\ensure... ...\displaystyle{R_\ell}}}}{{\ensuremath{\displaystyle{\sigma_{R_\ell}^2}}}}}}}=M$$

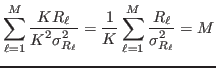
as if the intensities were simply counts. Therefore $K$ is given by

$$K={\ensuremath{\displaystyle{\frac{{\ensuremath{\displaystyle{ 1 ... ...h{\displaystyle{R_\ell}}}}{{\ensuremath{\displaystyle{\sigma_{R_\ell}^2}}}}}}}$$

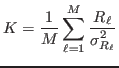
In output then we give 3-column files with columns

$$\hat{B}_\ell, \quad KR_\ell, \quad K\sigma_{R_\ell}$$