Here we explore some special cases to see the robustness of the method.
1) If no experimental observation contributes to bin ![]() according to one of the criteria
above, then we shall find
according to one of the criteria
above, then we shall find ![]() and especially
and especially ![]() . The latter condition is
valid as an exclusion condition
(meaning that we discard that point and we do not perform further operations on it,
neither do we output it).
. The latter condition is
valid as an exclusion condition
(meaning that we discard that point and we do not perform further operations on it,
neither do we output it).
2) if only one experimental observation - call it interval ![]() , dropping indices - contributes
to bin
, dropping indices - contributes
to bin ![]() ,
then we have
,
then we have
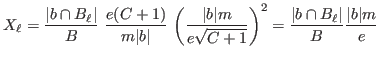
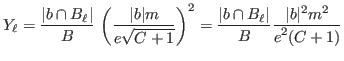
and so
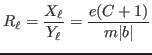
that is the experimental rate as in pixel
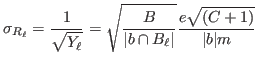
that is the same s.d. that can be calculated directly for
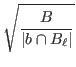
that takes into account the extrapolation error.