


Next: Basic binning
Up: Introduction
Previous: Notation
Contents
The physical observable of interest in any scattering experiment is [1-3] the differential cross section
as a function of direction 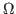 .
To measure that directly we should operate with zero-width point detectors, with instant measurement and unit incident intensity.
Practically
the quantity we can actually measure - putting a detector in a position covering a certain
solid angle for a certain time with a certain incident intensity - is
.
To measure that directly we should operate with zero-width point detectors, with instant measurement and unit incident intensity.
Practically
the quantity we can actually measure - putting a detector in a position covering a certain
solid angle for a certain time with a certain incident intensity - is
If 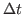 ,
,
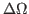 are small and known and
are small and known and 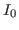 is separately monitored,
we can (have to) normalize the observations by simply dividing them out.
is separately monitored,
we can (have to) normalize the observations by simply dividing them out.
Specifically for the powder diffraction field, historically, this is not usually done because
- as it is normally true with anode sources and point detectors and usual procedures -
the counting times 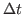 , the solid angle width
, the solid angle width
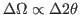 and the incident intensity
and the incident intensity 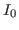 are considered
constant and therefore go into some 'global scaling' constant that is usually considered arbitrary.
are considered
constant and therefore go into some 'global scaling' constant that is usually considered arbitrary.
However, as we have more sophisticated acquisition methods,
we may need revert to the original approach and consider the
counts divided by time and angular width as the real observable.



Next: Basic binning
Up: Introduction
Previous: Notation
Contents
Thattil Dhanya
2019-04-08
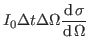
![]() , the solid angle width
, the solid angle width
![]() and the incident intensity
and the incident intensity ![]() are considered
constant and therefore go into some 'global scaling' constant that is usually considered arbitrary.
are considered
constant and therefore go into some 'global scaling' constant that is usually considered arbitrary.