Analytical comparison of averages

First we give an analytical comparison between simple average and Mighell-Poisson weighted average for $N_{\mathrm{obs}}=2$ . If the two events are $C_1$ and $C_2$ , then

$$\langle x \rangle={\ensuremath{\displaystyle{\frac{{\ensuremath{\... ...nsuremath{\displaystyle{\sqrt{C_1+C_2}}}}}{{\ensuremath{\displaystyle{2}}}}}}}$$

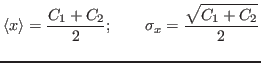
For the M-P weighted average,

$$\langle x \rangle_{\mathrm{w(2)}}={\ensuremath{\displaystyle{\fra... ...{\displaystyle{(C_1+1)(C_2+1)}}}}{{\ensuremath{\displaystyle{C_1+C_2+2}}}}}}}}$$

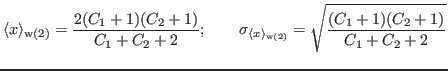
Now, supposing that the common 'true' value of $C_1,C_2$ is $\lambda$ , we use the Poisson distribution to compare the expectation values of the two results. The expectation value of the simple average is

$$E{\ensuremath{\left({\langle x \rangle}\right)}} = \mathop{\sum}_... ...ath{\mathrm{e}}}^{-\lambda}}}}}{{\ensuremath{\displaystyle{n!}}}}}}} =\lambda$$

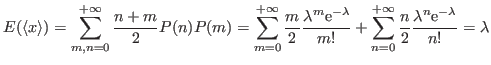
As expected, the simple average gives the true value. For its variance,

$$E{\ensuremath{\left({\sigma_x^2}\right)}} = \mathop{\sum}_{m,n=0}... ...ac{{\ensuremath{\displaystyle{\lambda}}}}{{\ensuremath{\displaystyle{2}}}}}}}}$$

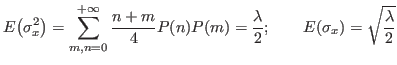
In order to evaluate the difference with the M-P weighted average, we rewrite the latter as

$$\langle x \rangle_{\mathrm{w(2)}}=\langle x \rangle + 1 -{\ensure... ...style{(C_1-C_2)^2}}}}{{\ensuremath{\displaystyle{4(\langle x \rangle+1)}}}}}}}$$

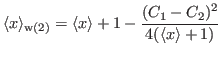
and calculate the expectation value of the last term:

$$E{\ensuremath{\left({{\ensuremath{\displaystyle{\frac{{\ensuremat... ...uremath{\displaystyle{\lambda^{n+m}}}}}{{\ensuremath{\displaystyle{n!m!}}}}}}}$$

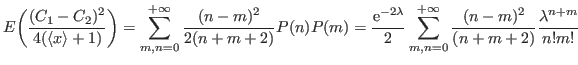
Rearranging the sums with $s=n+m$ , $s=0\ldots +\infty$ ; $n-m=s-2k$ , $k=0\ldots s$ , we get

$$E{\ensuremath{\left({{\ensuremath{\displaystyle{\frac{{\ensuremat... ...hrm{e}}}^{-2\lambda}}}}}{{\ensuremath{\displaystyle{4\lambda^2}}}}}}} %{n!m!}$$

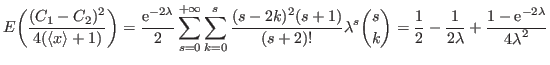
So, the relative difference between averages is

$${\ensuremath{\displaystyle{\frac{{\ensuremath{\displaystyle{E{\en... ...math{\mathrm{e}}}^{-2\lambda}}}}}{{\ensuremath{\displaystyle{4\lambda^3}}}}}}}$$

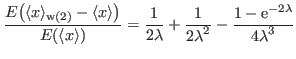
The relative error on $\langle x \rangle$ is

$$\epsilon = {\ensuremath{\displaystyle{\frac{{\ensuremath{\display... ...suremath{\displaystyle{1}}}}{{\ensuremath{\displaystyle{\sqrt{2\lambda}}}}}}}}$$

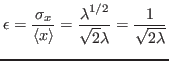
therefore

$${\ensuremath{\displaystyle{\frac{{\ensuremath{\displaystyle{E{\en... ...aystyle{E{\ensuremath{\left({\langle x \rangle}\right)}}}}}}}}}= O(\epsilon^2)$$

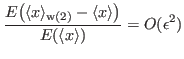
Therefore, the expectation value of the error (relative) involved in taking the M-P weighted average instead of the simple average is negligible.