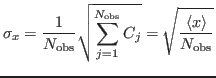Suppose we have
![]() Poisson-variate experimental evaluations
Poisson-variate experimental evaluations
![]() ,
of the same quantity
,
of the same quantity ![]() .
There are different ways to obtain from all
.
There are different ways to obtain from all
![]() data values a single estimate of the observable which is better than
any of them. The most straightforward and the best is the simple average
data values a single estimate of the observable which is better than
any of them. The most straightforward and the best is the simple average
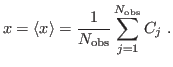
As the sum of Poisson variates is a Poisson variate, the standard deviation
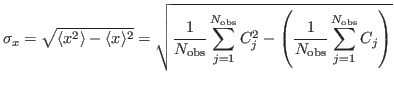
can be evaluated more comfortably as