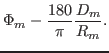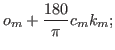


Next: How are different positions
Up: Angular conversion
Previous: Angular conversion
Contents
How is the channel number coverted into angle?
Mythen II modules are composed by 1280 pixels, each having width p=0.05 mm, and numbered with j=0,..,1279.
Angles are counted counterclockwise from the beam direction. For the m-th module, the angle
 of its j-th pixel center
can be determined using the three geometric parameters
of its j-th pixel center
can be determined using the three geometric parameters 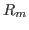 [mm],
[mm], 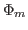 [deg],
[deg], 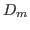 [mm], as in Fig.
[mm], as in Fig. ![[*]](crossref.png) .
The detector group uses instead the 3 parameters center
.
The detector group uses instead the 3 parameters center 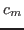 [ ], offset
[ ], offset 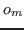 [deg], conversion
[deg], conversion 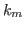 [ ].
The law with the 3 geometric parameter is
[ ].
The law with the 3 geometric parameter is
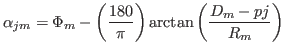 |
(5.1) |
The corresponding law using DG's parameters is
![$\displaystyle \alpha_{jm}=o_m+{\ensuremath{\left({{\ensuremath{\displaystyle{\f...
...t)}}\arctan{\ensuremath{\left[{{\ensuremath{\left({j-c_m}\right)}}k_m}\right]}}$](img49.png) |
(5.2) |
One can convert the two forms by equating separately the term out of the arctan and the argument of arctan for two different values of j.
It results
Conversely,



Next: How are different positions
Up: Angular conversion
Previous: Angular conversion
Contents
Thattil Dhanya
2019-04-08
![[*]](crossref.png) .
The detector group uses instead the 3 parameters center
.
The detector group uses instead the 3 parameters center ![]() of its j-th pixel center
can be determined using the three geometric parameters
of its j-th pixel center
can be determined using the three geometric parameters ![]() [mm],
[mm], ![]() [deg],
[deg], ![]() [mm], as in Fig.
[mm], as in Fig. ![[*]](crossref.png) .
The detector group uses instead the 3 parameters center
.
The detector group uses instead the 3 parameters center ![]() [ ], offset
[ ], offset ![]() [deg], conversion
[deg], conversion ![]() [ ].
The law with the 3 geometric parameter is
[ ].
The law with the 3 geometric parameter is
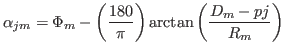
![$\displaystyle \alpha_{jm}=o_m+{\ensuremath{\left({{\ensuremath{\displaystyle{\f...
...t)}}\arctan{\ensuremath{\left[{{\ensuremath{\left({j-c_m}\right)}}k_m}\right]}}$](img49.png)