Theory

The Mythen Detector is used for powder diffraction experiments. In powder diffraction experiments the sample’s diffraction pattern is measured. Based on Bragg’s Law (1) the material (crystaline) structure can be reconstructed.

(1)\[2*\theta_{B} = 2*\arcsin\left(\frac{n\lambda}{2q}\right),\]

where \(\theta_{B}\) is the diffraction angle, \(\lambda\) the wavelength of the laser beam, \(n\) the diffraction order and \(q\) the grating constant of the crystal.

Fig. 1 Example of Diffraction Pattern taken with Mythen detector (only one detector module is shown).

One can use simple trigonometric relations to deduce the diffraction angle \(\theta_{B}\) from the geometric parameters of the detector such as the detector position relative to the sample and the intrinsic detector parameters (e.g. chip width, chip arrangement). The diffraction angle is thus a function of the strip/chip index and the detector geometric’s parameter \(\sum\). An example of possible detector parameters is shown in Fig. 2.

\[\theta_B = f_{\sum}\left(\textrm{strip_index}\right)\]

Detcetor parameters

A schemantic representation of Mythen’s detector setup is shown in Fig. 2. The Mythen detector consists of multiple modules arranged in a circular fashion. Each module consists of 1280 chips commonly referred to as strips or channels. Each strip has a width of 0.05 mm also referred to as pitch. The detector can be rotated around the sample. Note that the rotation trajectory is generally not equivalent to the detector’s circumference.

Fig. 2 Schemantic representation of Mythen detector setup. The diffraction angle \(\theta_B\) depends on the three geometric parameters \(R\), \(D\) and \(\phi\).

In Fig. 2 the parameter \(R_m\) represents the ortogonal sample projection onto the module plane, parameter \(D_m\) represents the distance of the first chip within the module to the sample projection and \(\theta_m\) represents the angle between the orthogonal sample projection and the direction of the laser beam. Note that these parameters differ for each module \(m\) but are rotation invariant for rotations around the sample \(S\). Using the above mentioned parameters \(\sum\), also referred to as module parameters, the diffraction angle can be calculated as follows:

(2)\[\theta_B = \phi_m - \arctan\left(\frac{D_m - \textrm{strip_index} * p}{R_m}\right),\]

where p denotes the pitch (internal detector parameter) and \(\textrm{strip_index} \in \{0,1,\cdots,1279\}\). Note that there are many more parameter sets to calculate the diffraction angle from. See section Different Parameter Sets for an overview of common parameter sets.

Note that due to sample displacement, error in wavelength and zero offset the measured diffraction pattern is prone to errors. The detector’s module parameters are thus slightly off and need to be calibrated for each module seperately.

Different Parameter Sets

In the previous section the parameterset \(\sum(R_m, D_m, \theta_m)\) was introduced. We refer to those as the “easy” EE parameters, as they have an easy underlying geometric representation.

DG Parameters:

Another parameter set are the DG “detector group” parameters \(\sum(c_m, k_m, o_m)\). These parameters were used during the initial developement of the Mythen Detector. We refer to \(c_m\) as center, \(o_m\) is refered to as offset and \(k_m\) as conversion. The DG parameters don’t have a trivial underlying geometric representation. The conversions between the DG parameters and EE parameters are given in (3).

(3)\[\begin{split}\begin{align} o_m &= \phi_m - \frac{D_m}{R_m} & \qquad \qquad \qquad \phi_m &= o_m + c_m k_m \\ k_m &= \frac{p}{R_m} & \qquad \qquad \qquad R_m &= \frac{p}{k_m} \\ c_m &= \frac{D_m}{p} & \qquad \qquad \qquad D_m &= c_m p \\ \end{align}\end{split}\]

Note

The conversion \(k_m\) is a positive number. Typically it is multiplied by a sign - which indicates if a module has been flipped. While in Fig. 2 the strips are indexed from \(0 - 1279\) and the photon counts are written to the file following this indexing. However, one can flip the modules and photon counts for strip index 1279 are written first to file. One thus needs to reverse the indexing such that equation (2) still holds. In the above equation the unsigned conversion \(k_m\) is used. For the EE parameters \(R_m\) and for the BC parameters \(L_m\) are positive values and can be multiplied by a sign.

The formula for the diffraction angle using DG parameters is as follows:

\[\theta_B = o_m + c_m k_m - \arctan(k_m(c_m - strip\_index))\]

BC Parameters:

Another parameter set are the BC “best computing” parameters \(\sum(\Psi_m, L_m, \delta_m)\). \(L_m\) denotes the distance of the module center to the sample. The angle \(delta_m\) denotes the angle between the module center and the orthogonal projection of the sample onto the module. And the angle \(\Psi_m\) denotes the angle between the center of the module and the direction of the beam. See Fig. 3 for a schemantic representation of the BC and EE parameters for one module.

Note that \(\Psi_m\) is completely independant from the other parameters and only depend on the module center and the beam direction. It can thus be redefined independantly. Therefore the parameters are called “best computing” parameters.

Fig. 3 Schemantic Representation of BC parameters and EE parameters for one module.

The conversion from EE to BC parameters and vice versa are given in equation (4).

(4)\[\begin{split}\begin{align} \phi_m &= \Psi_m + \delta_m &\qquad \qquad \qquad \Psi_m &= \phi_m - \arctan\left(\frac{D_m - U}{R_m}\right) \\ R_m &= L_m\cos(\delta_m) &\qquad \qquad \qquad L_m &= \sqrt{{R_m}² + (D_m - U)^{2}} \\ D_m &= L_m\sin(\delta_m) + U & \qquad \qquad \qquad \delta_m &= \arctan{\left(\frac{D_m - U}{R_m}\right)} \\ \end{align}\end{split}\]

\(U\) denotes the module center \(1279 \cdot 0.5\cdot p\).

The conversion from BC to DG parameters are given in equation (5):

(5)\[\begin{split}\begin{align} \Psi_m &= o_m + \frac{180}{\pi} cm km - \arctan((cm - 0.5\cdot N)k_m) &\qquad \quad o_m &= \Psi_m + \delta_m - \frac{180}{\pi} \frac{L_m \sin(\delta_m) + U}{L_m \cos(\delta_m)} \\ L_m &= \frac{p}{k_m}\sqrt{1 + (k_m(c_m - 0.5 \cdot N))^{2}} &\qquad \quad k_m &= \frac{p}{L_m \cos(\delta_m)} \\ \delta_m &= \arctan\left((cm - 0.5 \cdot N)k_m \right) &\qquad \quad c_m &= \frac{L_m\sin(\delta_m) + U}{p}, \end{align}\end{split}\]

where \(N\) denotes the number of strips in the module, thus 1280.

The diffraction angle is given as:

\[\theta_B = \Psi_m + \delta_m - \arctan\left(\frac{L_m \sin(\delta_m) + U - p \cdot strip\_index}{L_m \cos(\delta_m)} \right)\]

Calculating the Diffraction Pattern from the Raw Intensity Spectrum

To obtain the diffraction pattern from the raw intensity spectrum the raw photon counts are corrected and then redistributed to fixed angle width bins.

Raw Photon Count Correction

Normalizing Distribution:

Note that the photon counts are Poisson distributed. We thus apply Mighell’s statistics to later use the Pearson \(\chi²\) goodness-of-fit criterion:

\[I = I + \min(I, 1)\]

The photon counts are now normal distributed. Note, as one almost never has photon counts smaller than 1 or if so, one detects them as a bad channel the variance and expected value simplifies to \(\sigma² = I + 1\) and \(\mu = I + 1\). See Section \chi²- similarity criterion for more details on the Pearson \(\chi²\) goodness-of-fit criterion:

Further the raw normalized photon counts are corrected as follows:

Rate Correction: First the raw photon counts are rate corrected by the exposure time \(\tau_e\) and the dead time \(\tau_d\). The rate corrected photon counts \(I_{rc}\) are given by:

\[I_{rc} = I \cdot \frac{1}{\tau_e} \cdot \frac{C}{C(\tau_d)},\]

where \(C [1/s]\) is the actual count rate. \(C(\tau_d) [1/s]\) is the apparent count rate measured by the detector and dependant on the dead time, which is given by the following formula:

(6)\[C(\tau_d) = Ce^{- C \cdot \tau_d}.\]

To obtain the actual count rate, we assume \(-C\cdot\tau_d \equiv W\). Equation (6) then becomes:

\[-\tau_d \cdot C(\tau_d) = We^{W},\]

W is thus given by the inverse Lambert W function of \(-\tau_d \cdot C(\tau_d)\), which we calculate numerically. The dead time \(\tau_d\) has been evaluated experimentally.

Incident Intensity Correction:

The photon counts are corrected by the theoretical incident intensity \(I_{0}\). The incident intensity is the theoretical intensity of the laser beam. \(I_{0,1s}\) is the incident intensity of the first acquisition divided by the exposure time \(\tau_{e}\).

\[I_{I_0,corr} = I * \frac{I_{0,1s}{I_0}\]

Solid Angle correction:

Don’t know what this is. Something to do with actual illuminated surface (transverse width of beam). Pixel height.

Flatfield Correction:

The photon counts are corrected by the flatfield values \(F\):

\[I_{f, corr} = \frac{I}{F}\]

The corrected photon counts \(I_{corr}\) are thus:

\[I_{corr} = (I + 1) * c,\]

where \(c\) is the product of all correction factors:

\[c = \frac{1}{I_0} * \frac{1}{F}.\]

Note that the variance and expected value then results to \(\sigma_{corr}² = c*I_{corr}\) and \(\mu_{corr} = I_{corr}\). `

MMh i dont know if the correction coefficient’s are constants or also probablistic variables. - The flatfield for sure is.

Conversion to fixed angular strip width bins

Based on the module’s parameters one can now convert the strip index to the diffraction angle. However, depending on the location of the strip one strip can cover a larger angular region than others. See Fig. 4. Additionally the angular width of a strip can be quite large. Thus, to get a more fine grained diffraction pattern we redistribute the photon intensity per strip to small resolution histogram bins covering a fixed angle.

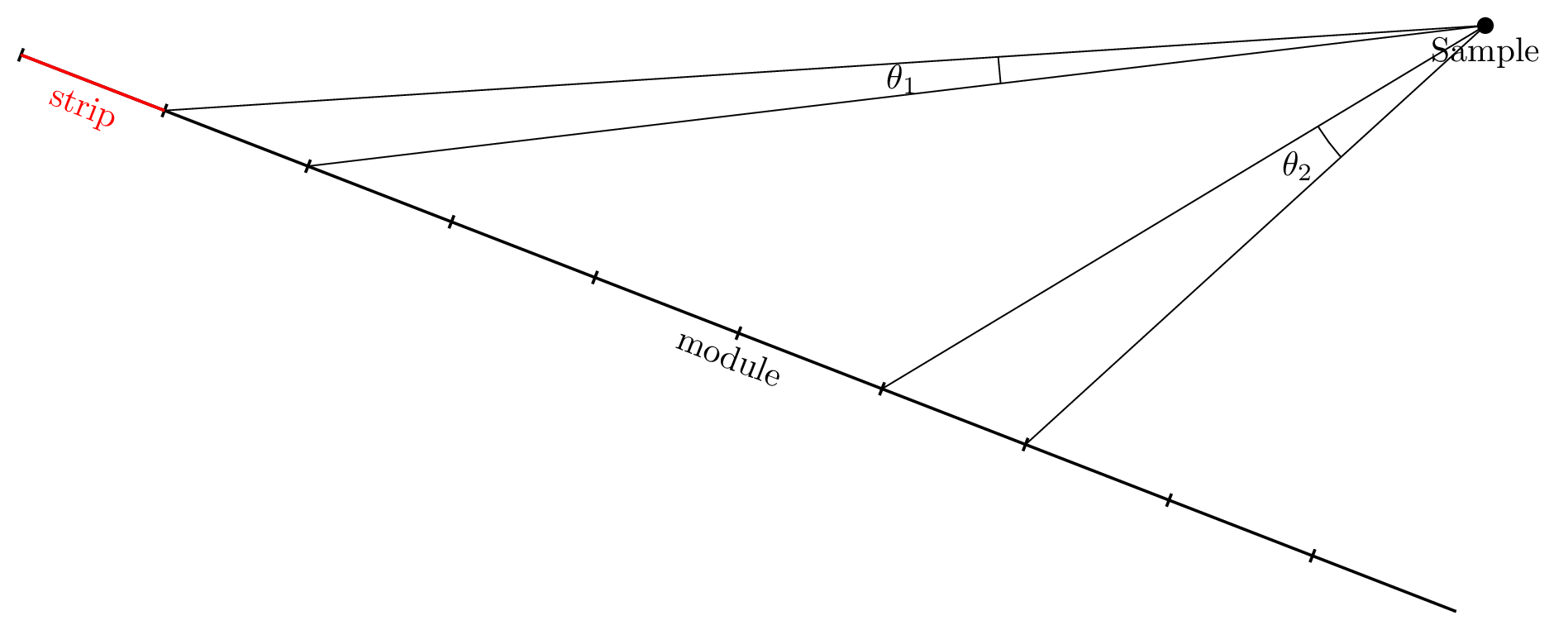
Fig. 4 Depending on the strip position relative to the sample the covered strip angle is much larger \(\theta_2 > \theta_1\).

The redistributed photon intensity \(I_{red, i}\) at fixed angle width bin \(i\) is given by:

\[I_{red, i} = I_{corr}*\frac{w_{bin}}{w_{strip}},\]

where \(I_{corr}\) are the corrected photon counts, \(w_{bin}\) is the histogram bin width denoted as an angle and \(w_{strip}\) the strip width denoted in angles.

The strip width \(w_{strip}\) for strip width index \(si\) is given as the difference in diffraction angle of the strip’s start \(\theta_{B_{si - 0.5}}\) and endpoint \(\theta_{B_{si + 0.5}}\):

\[\begin{split}\begin{align} w_{strip}(si) &= \phi_m - \arctan\left(\frac{D_m - (si + 0.5) * p}{R_m}\right) - \left(\phi_m - \arctan\left(\frac{D_m - (si - 0.5) * p}{R_m}\right)\right) \\ &= \arctan\left(\frac{D_m - (si - 0.5) * p}{R_m}\right) - \arctan\left(\frac{D_m - (si + 0.5) * p}{R_m}\right) \end{align}\end{split}\]

The resulting variance is then given as:

\[\sigma_{red, i}^{2} = \sigma_{red, i}^{2}\left(\frac{w_{bin}}{w_{strip}}\right)^{2}\]

Note that several strip widths might overlap with one bin. Nor might a strip cover the entire bin. We thus use the weighted average of all the corrected photon counts of strip’s, where the strip overlaps with the bin \(T\):

\[T = \left\{si \in \{0, \dots, 1279\} | \left[\theta_{B_{si- 0.5}}, \theta_{B_{si + 0.5}}\right] \cap \left[(i - 0.5)*w_{bin}, (i + 0.5)*w_{bin}\right] \neq \emptyset \right\}\]

The weighted average is then given by:

\[I_{red, i} = \sum_{si \in T} \alpha'_{si, i} * I_{corr}(si),\]

where the normalized statistical weights \(\alpha'_{si,i}\) are given by:

\[\alpha'_{si, i} = \frac{c_{si,i} * \sigma_{corr}^{-2}(si)}{\sum_{si \in T} c_{si,i} * \sigma_{corr}^{-2}(si)}.\]

The parameter \(c_{si, i}\) denotes the bin coverage factor e.g. how much of the bin is covered by the strip:

\[ c_{si, i} = \frac{\min(\theta_{B_{si + 0.5}}, (i + 0.5)*w_{i}) - \max(\theta_{B_{si - 0.5}}, (i - 0.5)*w_{i}) }{w_{i}}.\]

Despite charge sharing, we assume that the photon counts per strip \(si\) are independant of each other. The resulting variance for the redistributed photon counts is then given by:

\[\sigma_{red, i}² = \sum_{si \in T} (\alpha'_{si, i})^{2} * \sigma_{corr}^{2}(si).\]

Parameter Calibration

In order to calibrate the module’s parameters we choose one of the peaks in the diffraction pattern, also referred to as base peak. The base peak is denoted by the peak’s central diffraction angle \(\alpha\). An example of a base peak is depicted in Fig. 6. We take several acquisition’s of the same sample, however with slightly shifted detector position. We shift the detector position by rotating the detector around the sample. Remember that the module’s parameters are rotation invariant. In theory this results in the same diffraction pattern as well as the same base peak just shifted by the rotation angle, in practice the diffraction patterns are slightly off. See Fig. 7 for an example of overlapping base peak regions. We thus minimize the Pearsons \(\chi²\)-similarity of the shifted acquired base peaks within one module to get the optimal parameters for each module.

Fig. 5 Diffraction pattern for module 0.

Fig. 6 Selected base peak around \(-49.4786^{\circ}\) for a single acquisition of module 0.

Fig. 7 Two base peaks of different acquisitions but for the same module 0.

To choose the base peak one can either use a tabulated Bragg’s angle known by the theoretical structure of the sample or qualitatively select a base peak in the measured diffraction pattern. Note that by rotating the detector around the sample the base peak should be measured by each module multiple times. However, the rotation range is limited by the detector setup and the angular range is usually much smaller than \([-180^{\circ}, 180^{\circ}]\). Therefore, choose a base peak angle that can be measured by all modules and is well within the detector rotation range.

\(\chi²\)- similarity criterion

Let \(ROI_{\alpha} = \{ \{I_{red,0}, \sigma^{2}_{red,0} \cdots , \{I_{red,N}, \sigma^{2}_{red,N} \} \}\) denote redistributed photon intensities within the base peak region of interest, where \(N\) is the number of bins covered by the base peak region. With M acquisition’s we have \(M\) regions of interests.

We now want to minimize the Neyman (variance-weighted) \(\chi²\)-similarity criterion:

\[\chi^{2}_{k} = \sum_{j=1}^M \frac{(I_{red, k, j} - \mathbb{E}_{k}(\sum))^{2}}{\sigma_{k}^{2}(\sum)},\]

where \(I_{red,k,j}\) is the redistributed corrected photon intensity for fixed angle width bin \(k\) and acquisition \(j\), \(\sigma_{k}^{2}(\sum)\) and \(\mathbb{E}_{k}(\sum)\) denote the variance and expected value for the bin \(k\) using the module parameters \(\sum\). With the module’s parameter set \(R\), \(D\) and \(\phi\) these are:

\[\sigma_{k}^{2}(R, D, \phi) = \sigma_{red, k,j}^{2}\]

MMh im confused - the observed values also depend on the module parameters. Also why isnt it a fixed variance expecting for bin k?

The expected value which minimizes the \(\chi²\)-similarity criterion is given by the weighted average of all observed values:

\[a_{min,k} = \mathbb{E}_{k}(R, D, \phi) = \frac{\sum_{j=1}^M I_{red, k, j} * \sigma_{red, k, j}^{-2}}{\sum_{j=1}^M \sigma_{red, k, j}^{-2}}.\]

and resulting variance:

\[\sigma_{a_{min,k}} = \frac{1}{\sum_{j=1}^{M} \sigma_{red,k,j}^{- 2}}.\]

The average \(\chi_k^{2}|a_{min,k}\) is then given by the average residual \(av\_res_{k}\):

\[av\_res_{k} = \sqrt{\frac{1}{M-1} * \chi_k^{2}|a_{min,k}} = \sqrt{\frac{1}{M - 1}*(S_{2,k} -S_{1,k}*S_{0,k}^{-1})},\]

with:

\[S_{p,k} = \sum_{j=1}^M I_{red, k, j}^{p} * \sigma_{red, k, j}^{-2}\]

We then scale the variance \(\sigma_{a_{min,k}}\) by the average residual. The scaled variances are then summed up for each bin within the base peak region.

We then get the similarity criterion for different base peak regions:

\[\sum_{k=1}^{N} av\_res_{k} * \sigma_{a_{min,k}}\]

The goal is to minimize this similarity criterion based on the module parameters \(\sum\).